Adam fecit 21 / Nel nono libro di “De Architectura” Vitruvio illustra la costruzione di una meridiana

Dopo la raccolta in un volume delle prime venti riflessioni sulle meridiane e sulle questioni astronomiche connesse (pubblicate dalla nostra testata dal 2018 al 2023), l’ing. Nino Ortolani riprende oggi la rubrica “Adam fecit” ricominciando, in un certo senso, dall’inizio. Prendendo spunto infatti da una edizione del Seicento del “De Architectura” di Vitruvio (il noto scrittore-architetto romano vissuto nel primo secolo A.C.), ci parla del libro nono dell’opera, quello in cui l’autore illustra dettagliatamente la costruzione di una meridiana solare. Interessanti anche le immagini che l’ing. Ortolani riprende dallo stesso volume del ’600, che riportano alcune scoperte e situazioni di illustri scienziati dell’antichità.

«Nobilibus Athletis qui Olimpia,… honores constituerunt…» (Ai nobili atleti vincitori nelle Olimpiadi gli antichi Greci conferirono grandi onori). Così ha inizio il libro nono del De Architectura di Vitruvio. E prosegue raccontando che «nel ritorno vittorioso al loro paese [i vincitori] fossero condotti in trionfo in una quadriga dentro e fuori la città, e godessero di una rendita a vita».

Nulla di nuovo sotto il sole se si pensa come sono accolti gli “atleti/eroi della nazionale” quando tornano vincitori di una partita di campionato. Non parliamo, poi delle “onorificenze”: alla fine di certe partite ci sono “premi” che superano quanto riceve, come “buonuscita”, un dipendente statale alla fine di una vita di lavoro.

Gli studiosi tenuti in minor considerazione degli atleti

Quanto sopra per esprimere la meraviglia «che questi stessi onori, e anche più grandi, non sono stati tributati agli scrittori che resero infiniti servigi per l’eternità all’umanità intera» come Platone, Pitagora, Archimede, ecc., di ciascuno dei quali riferisce alcune «riflessioni che sono di utilità per lo sviluppo della vita umana».

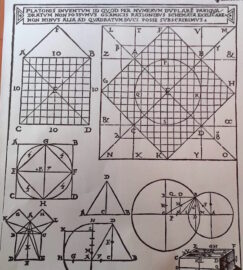
Platone dimostra graficamente come raddoppiare la superficie di un quadrato di cui si conosce la lunghezza del lato.

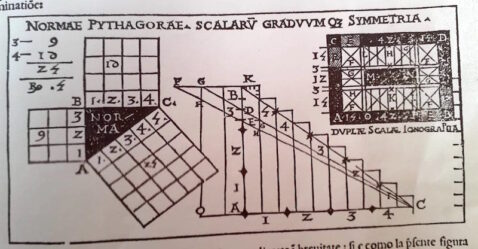
«Pitagora fece conoscere una squadra scoperta senza tecniche artigianali».

Di Archimede, «fra le tante sue straordinarie scoperte» viene illustrata la determinazione di quanto argento si trovava in una corona che «Ierone, innalzato al potere regale di Siracusa» aveva ordinato fosse solo in oro. Nel testo è illustrata, con dovizia di particolari, la soluzione scientifica conseguenza della scoperta della famosa “spinta che ricevono i corpi immersi in un fluido”. «Archimede, nell’uscire dalla vasca da bagno “nudus domum vadens versus” (andando nudo verso casa), gridava “eureka” (ho trovato)».

Il libro nono del “De Architectura” illustra la costruzione di una meridiana

Molte sono le traduzioni pervenuteci dal Seicento ai giorni nostri del capolavoro di Vitruvio. Ma non sempre si trovano corredate di grafici nonostante la dicitura del testo «uti descriptum est in una pagina» (come illustrato nella stessa pagina). Questo spiega le difficoltà delle traduzioni dei testi di natura scientifica del mondo classico: il “letterato” non sa di disegno e il tecnico non sa di “lettere”.

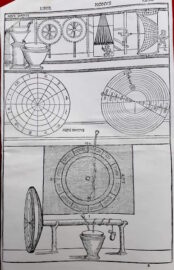
Dopo il lungo proemio viene illustrato il contenuto del libro nono: «teorie gnomoniche, ovvero lo studio delle ombre dello gnomone, “dilatentur aut contrahantur, explicabo” (spiegherò come si allungano o si accorciano) nei diversi giorni al variare delle stagioni».
La costruzione grafica di una meridiana è spiegata in modo dettagliato come a una classe di scuola media con riga e compasso. Ma il tutto è finalizzato a spiegare la misura del tempo (“che ora è?”, “che giorno è?”) per cui non poteva mancare la spiegazione di vari tipi di orologi tra cui (in mancanza di sole) i congegni ad acqua.

Nino Ortolani